Lessons for COVID-19 and Supply Chain Management Models

Summary

With the current COVID-19 challenges “models” have taken center stage. Models are being used for estimating the number of COVID-19 hospitalizations and deaths with and without mitigation, how much of each resource will be needed (ventilators, beds, PPE, testing, etc.), and now how to optimally handle economic reopening with minimizing COVID-19 health impacts. Based on over 500 years of SCM modeling experience at Arkieva there are some critical lessons that are crucial to maximizing success against COVID-19. The purpose of any model is not a perfect estimate of the future, but:

Insight into a business or health situation providing tools that help overcome human cognitive limitations
A structure to keep discussions about actions and policies organized
Identifying what data is available, what data is needed, and the delta between available and needed
The ability to compare / contrast / analyze different estimates of the future based on different models or different assumptions and use this to guide policy

There are three primary classes of computation models: High level (top-down), middle, and granular (bottoms up). Models for analysis typically start with the high and middle level – this is true for COVID-19. These models work fine to generate a high- level assessment and insight. Inevitably, detailed granular models are needed to work with the high-level models in a loosely coupled fashion to effectively support key decisions. In SCM this is often factory flows, inventory replenishment, detailed assessment of demand, etc. For COVID-19, these detailed models are critical to economic reopening decisions. The initial COVID-19 early requirement response was broad measures to quickly slow up the runaway train that was about to outstrip health care capacity, hence broad mitigation strategies without concern for the individual effectiveness. For a successful reopening detailed models are needed. Models that are often found in industry, but not in managing anything like COVID-19. This drives daily alert conditions, action plans, and assessments to ensure the government is focusing on keeping a COVID-19 outbreak from occurring. For example, rural area models for chicken farming as opposed to keeping folks from one state entering another state to purchase liquor and groceries, where the border between the two states has no geographic meaning.

Introduction

With the current challenges from COVID-19 – “models” have taken center stage for interest, importance, and criticism. In SCM (Back to the Basics: What’s the Core Purpose of Supply Chain Management?) we see this same jump in visibility when a challenge emerges (change in demand, production capability, supplier interruption, etc.) For COVID-19 arguably the mid-March model results estimating there could be 2 million deaths in the US put models front and center. It generated this initial response from Dr. Deborah Birx that the White House was looking at this, but “one has to be careful with models, modelers have a certain bias”. Since then models have been critical to

Assessing when will the APEX arrive for different areas.
When and how much medical equipment will be a need (Ventilators, beds, ICU beds, personal).
At what rate will COVID-19 decline (new cases, hospitalizations, ICU beds, and deaths).
How much and which kind of testing is needed when and where.
Supporting effective economic reopening.
1. What is the impact of pulling back from which mitigation efforts?
2. Identify “hot spots” before they become hot or at least an early warning system.
3. New mitigation actions to take to support reopening.
4. As COVID-19 actual numbers change, how do I use these to anticipate a spike, assess if I can reopen more, and/or determine what actions I need to take or data to collect?
5. Balancing risk and economic activity.
6. Assessing the reopening guidelines.
  - Hospitals in the state must be able to safely treat all patients requiring hospitalization, without resorting to crisis standards of care.
  - A state needs to be able to at least test everyone who has symptoms and will most likely need to test many that are non-symptomatic, more than once.
  - The state can conduct monitoring of confirmed cases and contacts.
  - There must be a sustained reduction in cases for at least 14 days.
7. Support managing the supply chain – better described as the demand-supply network to service COVID-19 patients and the economic reopening.

Given the importance of these questions and the political environment, models have become front and center in policy / political discussions, for example:

The recent exchange between President Trump and Governor Cuomo on whether NYS asked for more beds than it needed.
The current exchange between Governors and the Whitehouse on whether enough testing capacity now exists or not.

For those that work regularly in supply chain or managing the demand-supply network (DSN) models are commonplace to help with similar questions. This blog will provide some basics about models that all will find helpful. It will address an often-heard criticism that the models are worthless since the data is incomplete (as recently as last week in a Philadelphia COVID-19 briefing). It pulls from over five hundred years of industrial-strength modeling experience at Arkieva, where multiple experts at Arkieva have more than 40 years creating and deploying models that help improve organizational performance. The blog does not dive into the details of the current COVID-19 models (a later blog) but does provide an overview and detailed references and some recommendations.

Purpose and Value of a Model

The purpose of any model is not a perfect estimate of the future, but

Insight into a business or health situation providing tools that help overcome human cognitive limitations (Peter Norden)
A structure to keep discussions about actions and policies organized
Identifying what data is available, what data is needed, and the delta between available and needed
The ability to compare / contrast / analyze different estimates of the future based on different models or different assumptions and use this to guide policy

Example of insight and comparing estimates

The following example relevant to COVID-19 will make the purpose and value of models clear. Assume I have been collecting data about the number of new events per time bucket. For COVID-19 this might be COVID-19 positives, hospitalizations, ICU admissions, serious illness, or death. For managing demand-supply networks, it might be manufacturing excursions, delays in delivery of raw material, or changes in demand. For this example, assume the events are hospitalizations for COVID-19.

Learn More: Identifying the Unobvious with Supply Chain Modeling

Initially we have data for seven days (figure 1) and the critical question is to estimate the number of events per day over the next 25 days. Following the KISS rule (keep it simple stupid), we find the best fit straight line (figure 2), this has a high R-squared value (the higher the value the better the fit maximum value is 1). All the people in the room except 1, conclude this is great, we have an estimate and we are done. We are 98% confident this will be true.

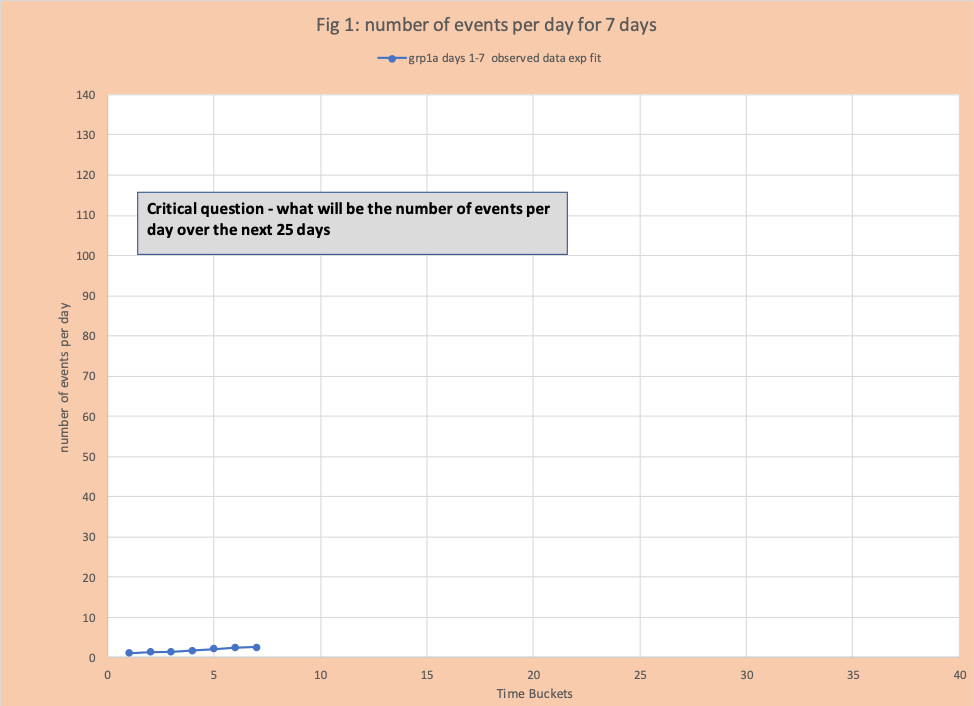
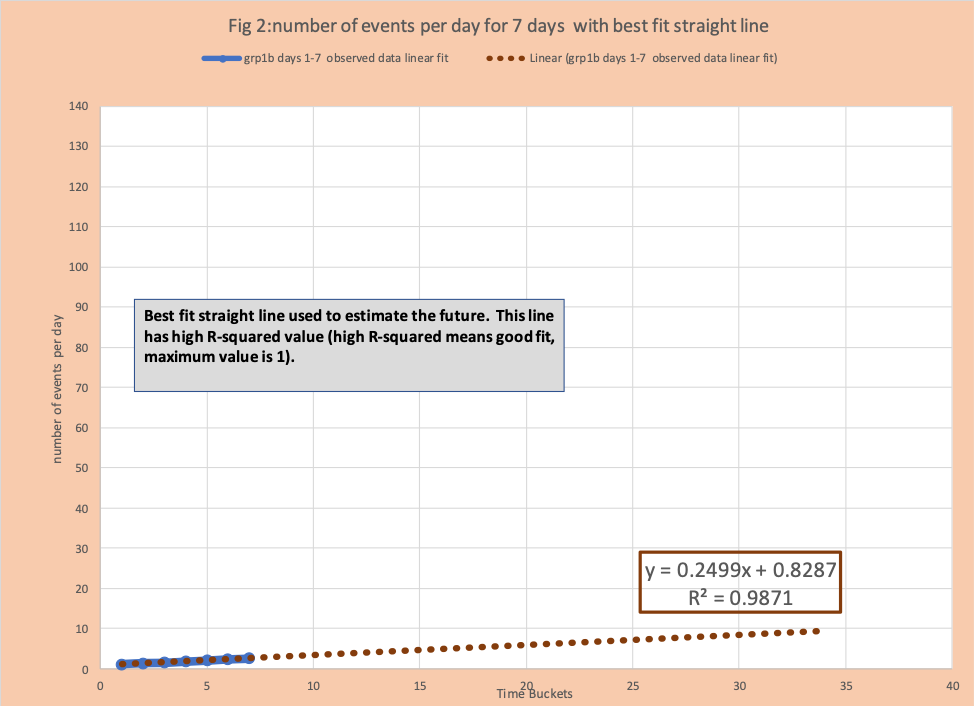
However, the crazy statistic person who wears a white robe (see Mark Twain The War Prayer) comes to the podium, takes control of the keyboard, and creates figure 3 which adds a second fit – exponential curve. This curve also has a high R-squared, but its prediction of future values is dramatically higher than the linear best fit. The robed stranger points out it might be prudent to prepare for this future outcome or at least monitor it regularly.

Which does the group choose? They ask the robed stranger which one is correct. The stranger informs them that it is impossible to know just using the data they have. One needs to step outside the data and apply community intelligence and risk analysis to make this decision. Quickly a subset of the group makes clear the KISS rule applies and the “statistics person” has no business sense and is just doing some fancy math. They aren’t statisticians, but they are smart folks- go with the linear estimate to show the boss that all is under control. The group pushing KISS insists all decisions must be data-driven only – which leads to the linear estimate. The robed stranger points out models are for insight, not exact decisions. The robed stranger is then banished for disloyalty and the linear estimate is taken to the executive.

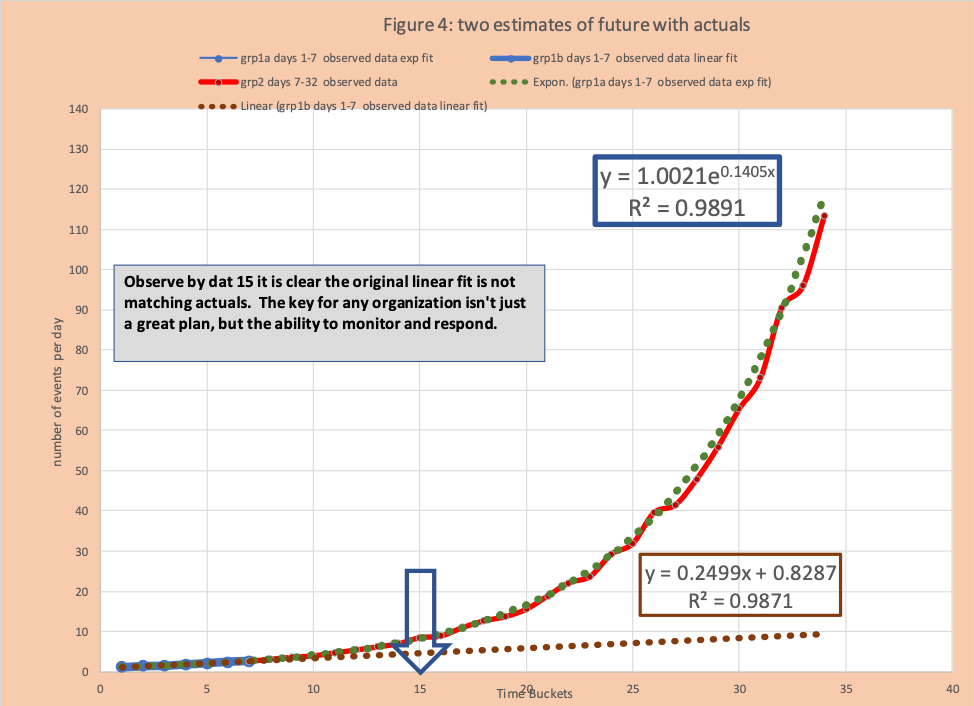
Figure 4 has actuals across the next 25 days. Alas the robed stranger was correct to consider the alternative exponential estimate and plan for the contingency. Critical was a failure to monitor the situation and adjust. By day 15 it is clear the original linear model is not accurate. The group that supported this was vested in protecting their recommendation and the voice of reason (robed stranger) had already been banished for failure to be loyal. This failure resulted in near bankruptcy for the organization. Luckily a Federal loan was secured to keep the firm afloat.

Basics of Models

In all models we have:

Players in the game.
1. COVID-19 players would be those susceptible to infection (S), exposed (E), infected (I) who can spread the disease, recovered (R) who can longer get the disease or spread it, and mitigation actions.
2. In SCM in supply or central planning, the players are the assets (capacity, existing inventory, etc.) and demand (for a product).
Relationships between the player that define the flow of activities.
1. For COVID-19 an infected person (I) can pass the virus to a susceptible person(s) and eventually moves to the recovered group (R). See Figure 1 in “Coronavirus and Analytics: Flattening the Curve”.
2. For supply or central planning this would be the path (bill of material) to purchase or produce products and assign them to meet demand. See Figure 1 in “Optimization and Central Planning: Compass or Advanced Navigation”.
Computational representation of the players and relationships to estimate future states.
1. COVID-19 – the number of events (positives, hospitalizations, ICU admits, recovery/deaths) per time-bucket (day, week, …) under different action plans.
2. SCM – Central Planning – projected supply linked to demand and workload on the demand-supply network.

Types of Computational Methods aka models

There are numerous types of methods and many ways to group them. We find the following non-technical grouping helpful.

Top-down – using data analysis (statistics and machine learning) to find patterns in data and then use this pattern to estimate the future for the entity that is the source of the data or a similar entity. This is sometimes called a statistical or data model.
Middle – capturing the players and interactions in a more aggregate mode than bottoms up, but more detail than in Top Down. The relationships are often represented with equations – for COVID-19 these are often differential equations.
Bottom-up – often called agents based in the infectious disease world. Granular representation of the players and their interactions with a stochastic (probability) component.

The following examples will provide clarity.

Learn More: Demand Forecasting Analytical Methods: Fit Vs. Predict

Top Down

For COVID-19 this computational method uses data analysis methods to find patterns in the data for an entity (for example number of hospitalizations per day in NYC) and then use these patterns to estimate future hospitalizations for NYC or use the pattern from NYC to help estimate the future in Philadelphia.

In SCM this is forecasting where a key concept is ‘fit and predict’. A critical insight from SCM for COVID-19 is data analytics methods for forecasting are by themselves only a component of estimating demand – called demand management.

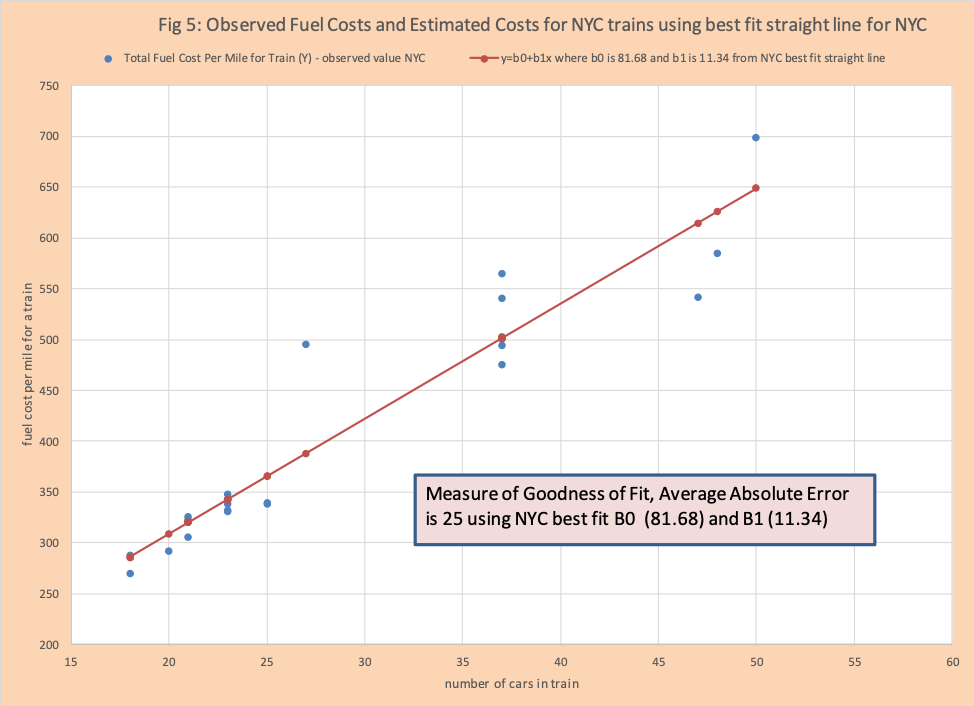
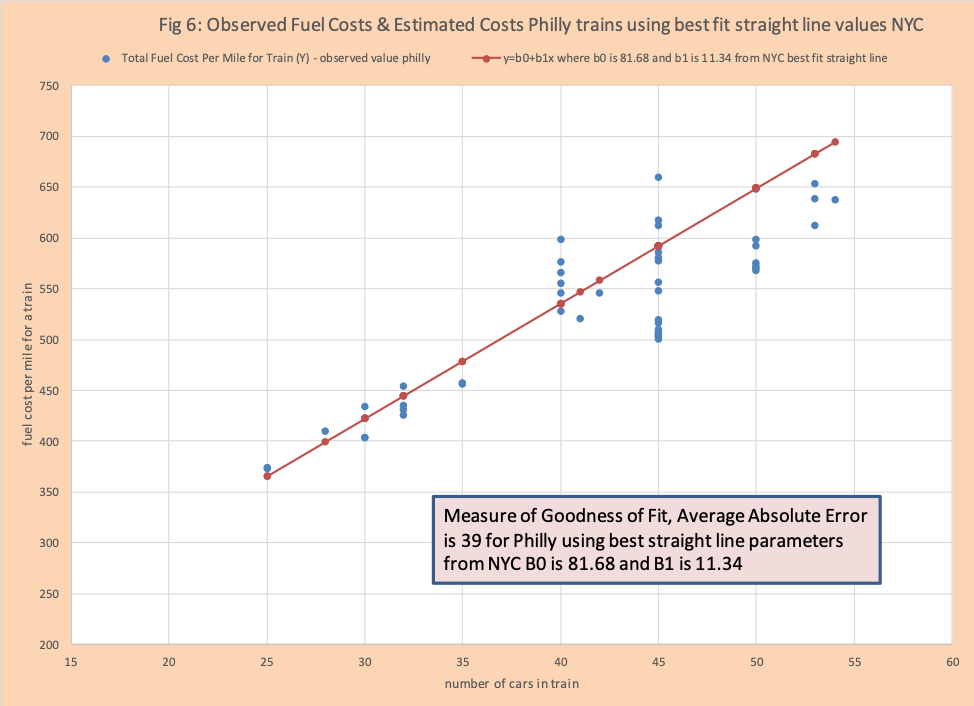
The following example will make “Top Down” clear. Assume that we would like to estimate the total fuel cost per mile for trains in Philly. We believe the critical factor or predictive variable is the number of cars on the train. We obtain 22 observations from NYC trains that have

The number of cars in the train (predictive or independent variable).
The fuel cost per mile (predicted or dependent variable).

We apply the optimization method linear least squares to find the best fit straight line (Y = B0 + B1*X). B0 is the y-intercept and B1 is the slope. Figure 5 has the observed data points plotted with the best fit straight line (B0 is 81.68 and B1 is 11.34).

We now need to estimate the fuel cost for 48 Philly based trains that run for the next 2 weeks where we are given the number of cars on each train. We use the same linear equation for NYC to estimate fuel costs for the Philly trains. Over these two weeks we capture the actual fuel costs. Figure 6 has the actuals plotted (scatter plot) with the predicted (straight line). The measure of the quality of this prediction is 39 compared to NYC which 25. Although the NYC prediction equation was helpful for Philly for a general trend, at a detail level its value was limited.

Learn More: Effective Approach to Mixing Judgment and Statistics in Forecasting

Middle

The best-known example of this set of methods is simultaneous equations. See example 1 in “Two Simple Examples to Help You Understand How Supply Chain Optimization Algorithms Work”

For COVID-19 the primary “middle” method are sets of differential equations. The differential refers to the rate of change at a point in time – for example acceleration (increasing or decreasing your car speed). In a differential equation the change is related to the current value. We refer the reader to work by Harrison Schramm

Coronavirus and Analytics: Flattening the Curve and its technical appendix and OR/MS Today Technical Appendix
COVID-19 Analysis and Policy Implications
Differential equation models for sharp threshold dynamics
“Epidemic Modeling: An Introduction” by Daley and Gani (Cambridge U. Press, 1999),
MAA material The SIR Model for Spread of Disease

For SCM, one of the primary methods is an optimization area named MILP (mixed-integer linear programming) that is often used in Central planning. See example 2 in “Two Simple Examples to Help You Understand How Supply Chain Optimization Algorithms Work” and “An Example of When Optimization Is Helpful in Supply or Central Planning.”

Bottoms UP

These models operate with more granularity and details of the interaction patterns than the other groups. Having been involved in building and deploying numerous factory and central planning models at all three levels – the need for granularity and details is inevitable as one first starts with models in the other two groups to get something operational quickly to provide insight. As an organization moves from needing some high-level insight to guide broad actions to insight into the impact of granular actions on organizational performance this drives the need for “Bottoms up” modeling.

Let’s return to the train example where the goal is to estimate fuel cost. The top-down model was less accurate for Philly, than NYC. Our analysis moved from “just the data we have” to understanding more about the players that impact fuel cost. The following predictor variable influence fuel costs.

Steepness of the Grade of the track.
1. NYC had mostly Steepness 1 – flat.
2. About half of the Philly trains had steepness 3 and 4, a good amount of steepness.
Engine type. There are three types that work better for trains with different lengths and steepness.
NYC had mostly engine types 1 and 2 optimally matched for number cars.
Philly had a number of trains that were not optimally matched with an engine.

Our analysis also found fuel cost estimates based on steepness, engine, and train size which could be used to create a bottom-up model.

For COVID-19 the early requirement was broad measures to quickly slow down the runaway train that was about to outstrip health care capacity. Hence broad mitigation strategies.

Only essential services could operate with their normal patterns, other businesses had to close or be work from home.
Close all schools and childcare centers except for critical employees.
Shelter in place except for critical travel (groceries, pharmacies, outside exercise at a distance.)

The broad measures supported by high-level models were late in taking measures to secure complete COVID-19 safety of seniors in elder care living facilities. Even today, in some states a resident in an elder care living facility that is sent to the hospital for COVID-19 treatment is returned to the same facility after making progress, but they are still COVID-19 positive. The broad measures failed to drive pre-emergence management in keeping COVID-19 spreads out of high-density work areas. Even as late as April 22, 2020 Delaware suffered a COVID-19 hotspot in the rural county of Sussex from chicken farming while devoting energy to keep citizens from Pennsylvania (which is a common economic unit with northern Delaware) from crossing the border to purchase food or liquor, but they are permitted to cross the border to work at the major health care centers.

Within these broad measures – differences occurred between states with common borders. In Delaware liquor stores remained open, they were closed in Pennsylvania. New Jersey banned non-essential driving after 8pm that was enforced by the police. Delaware and Pennsylvania did not. These three states have different rules on the usage of state and county parks.

As states move to reopen more detailed granular models will be critical. In the same manner, as firms need detailed models to work in a loosely coupled manner with high-level models for maximum effectiveness. (Decision Grids)

What is the right policy for liquor stores, and parks? How much social distancing is needed for youth soccer? What about the theatre?

Bottom-up models are common in the industry, but just starting to emerge for COVID-19.

Such models will help with pre-emergence management (chicken farms) and identify low-risk reopening (basketball rims at Skyline middle school).

For SCM, the examples are numerous and commonplace. Two examples:

In the production of cheese, the age of the cheese is critical to successful production and quality. In the production of shredded cheese, the age range to send the shredding machines is 3 to 9, with a preferred age of 3-4. However, a critical offset to optimizing to preferred age is protecting against a manufacturing excursion.
In Wafer fabrication (core component for laptops, cell phones, cars, …) the Semiconductor Supply Chain – Enterprise-Wide Planning Challenges one of the key toolsets is Photo. At an aggregate level of modeling, we use a production rate for these tools. However, in practice setup time and deployment are critical details. Setup times can be long and deployment limits which of the identical tools can handle which products.

References for detailed information on COVID-19 models

I have intentionally avoided any detailed discussion of the current COVID-19 models, simply outside the scope of this blog. Below are some references the reader will find helpful

Importance of data and data limitations

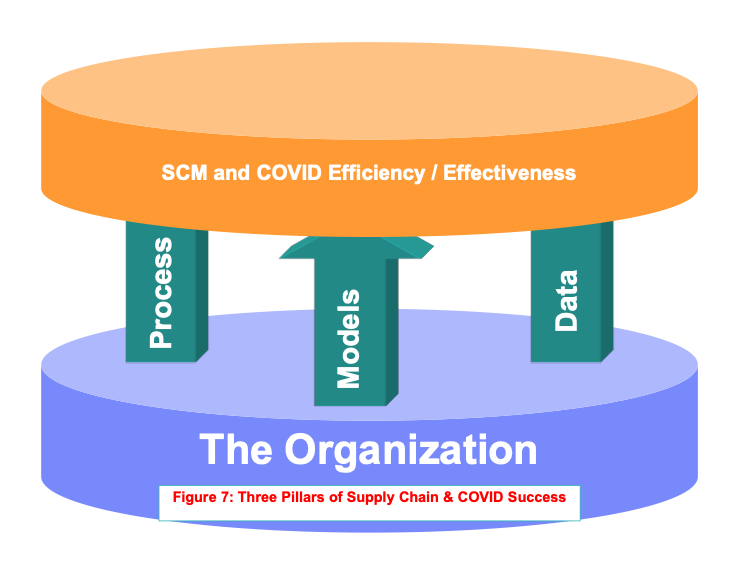
This is a critical area that will be addressed in a future blog. Data, Models, and business or COVID-19 processes are tightly coupled and interdependent. The data available and the current process is a starting point. Models are built which help adjust processes and identify data gaps. This iterative process is critical to improving organization processes (figure 7).

Stu Reed, then IBM Vice President, Integrated Supply-Chain Development and Deployment made the following remarks at the Edelman 2000 competition: “My job is to ensure excellence across IBM’s supply chains and communicate IBM’s intent to become a premier e-business. What we have here is a process transformation that was hardened by the application of information technology that was set upon the fundamentals of key operations research theory and—most importantly from my boss’s perspective—we created a lot of business value. The hard science is the basis for trust in the data. Without people trusting the data that came out of the central engine, the entire transformation would have been halted… We combined process reengineering cemented by the application of I.T. based on operations research hard science to bring true business value to the IBM Microelectronics Division.”

Click here for a good place to start to understand the limits of COVID-19 data.

Conclusion

COVID-19 and SCM models are critical cognitive tools to support effective decision making and navigate the efficiency frontier. As with SCM, COVID-19 will require the development and deployment of detailed models to operate at maximum efficiency. Three critical rules

“Simple solutions that sound rational at a first look are a dangerous distraction from the real work that needs to be done.”
Complexity exists, whether you recognize it or not, best to recognize it
The Models are Incomplete, the Intuitions are Unreliable

Enjoyed this post? Subscribe or follow Arkieva on Linkedin, Twitter, and Facebook for blog updates.