In this series of blog posts, we have been talking about Jane, who is in the role of inventory planner at her company, and Kate, a consultant, who has been helping Jane with the concepts.
Catch up on the first 8 parts: part 1, part 2, part 3, part 4, part 5, part 6, part 7, and part 8.
Kate pointed to the whiteboard, which had the following written on it:
Safety Stock = z-score * √[ {σDayDemand2*(L/1)} + {μDemand2 * σLeadTime2}]
Kate said, “I think of safety stock as z-score * √(σDDLT)2 or simply z * σDDLT where σDDLT is the standard deviation of demand during lead time. The z value is related to the service level and can be looked up on the internet via tables or calculated in Excel using the NORM.S.INV function. As far as the formula of σDDLT goes, right now, we have two terms in the formula of σDDLT. The first one is related to the variability in demand during average lead time; the second one is related to the fact that the lead time itself is variable. As I said earlier, as long as the quantities are independent, the variances can be added together. This means that if I have variance coming in from the supply side, say a variance between what was ordered versus what was received, it can be added into this formula. It will be one more number inside the square root.”
Jane looked a bit puzzled. She said, “Perhaps we can look at an example first before adding more things to the formula?”
Kate readily agreed. She asked Jane to pull up historical sales and lead time data for a particular product and calculate the average, standard deviation, and variance for these data points.
Jane provided the following table and calculations from Excel.
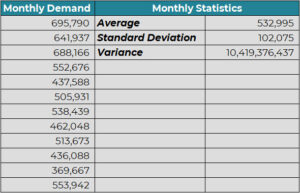
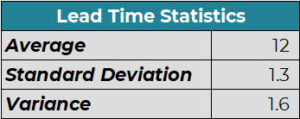
Kate looked at the table and noticed that the demand data was in months whereas the lead time was in days. She suggested that Jane convert the demand statistics from monthly to daily.
Jane said, “I know how to convert the monthly average to daily. But how about the variance and standard deviation?’
Kate replied, “Ideally, we would use the day-by-day demand data to calculate these statistics. But since we do not have this data, we will do the next best thing available to us. We will assume that the demand on a given day is independent of demand on any other day. With this assumption, we can stipulate that the monthly variance is the sum of 30 individual daily variances. So, the monthly variance can be converted to daily variance by dividing it by 30. And standard deviation is the square root of variance, so that is easy to calculate from there.”
Jane nodded and produced the following calculations.
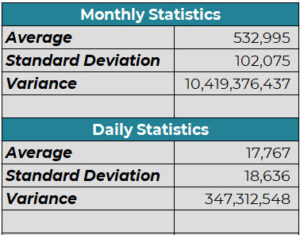
“Great!”, Kate exclaimed. “So the variance of the demand during lead time or (σDDLT)2 based on your numbers would be the variance of daily demand times average lead time plus Square of Average daily demand times Variance of lead time.”
She wrote on the whiteboard:
(σDDLT)2 = 347,312,548 * 12 + (17,767)2*1.6
= 4,074,243,350 + 499,155,026
= 4,573,398,377
And
σDDLT = √(4,573,398,377)
= 67,627
“Now”, Kate said, “what service level do we want to calculate the safety stock for?”
“I do not know. How about 90%? or 95%?”, Jane responded.
“Well, that is your or the business’s decision”, Kate replied. “The z value for 90% is 1.645. For 95%, it is 1.96. So, the safety stock will go up as the service level goes up. As it turns out, the safety stock for 90% service level will be 1.645*67,627 or 86,667 units. For a 95% service level will be 1.96*67,627 or 111,236 units. As you can see, a 5% increase in service level increases the safety stock by almost 25,000 units in this example”.
“Hmm, I see”, Jane demurred. “So, if I have the raw demand data for any product, and the lead time information, I can calculate the safety stock this way? That seems easy enough”.
Kate said, “I agree. It is easy enough once we make the assumptions that we have talked about so far. You may want to practice this with data for other products.”
We will continue the conversation in the next blog post.
Read the next blog in the series here.






