Summary
As the nation enters the ninth month of COVID-19 and it is clear this will play out for at least all of 2021, there are three primary themes: (a) controlling the spread while balancing the impact on people and the economy and finding the set of actions on the efficiency frontier, (b) actions that maintain quality hospital care in the wake of increasing utilization account for the operating curve, and (c) development, production, and distribution of the vaccines(s). Monte Carlo Discrete Event Computer Simulation (MCDECS) is a particularly powerful and flexible “tool of the trade” for a wide range of challenges in supply chain and operations management – from estimating capacity to setting COVID-19 protocols. This blog provides some basics on MCDECS, the next blog will use MCDECS to explain why limiting the size of a gathering helps reduce the spread of COVID-19.
Introduction
As the nation enters the ninth month of COVID-19 and it is clear this will play out for at least all of 2021, there are three primary themes: (a) controlling the spread while balancing the impact on people and the economy and finding the set of actions on the efficiency frontier (a future blog), (b) actions that maintain quality hospital care in the wake of increasing utilization account for the operating curve, and (c) development, production, and distribution of the vaccines(s). For good reason, folks have numerous questions – one that I came across the other day was “what is the value in limiting the size of gatherings”. In the process of creating an explanation for this question, I used the analytics method Monte Carlo Discrete Event Computer Simulation (MCDECS) developed by the OR/MS community with the advent of widely available general-purpose computers in the 1960s. Sargent provides a short history, with the simulation remaining a dominant analytics method. The purpose of this blog is a quick overview of MCDECS continuing our series on tools of the trade to support the next blog on the value of limiting the size of gatherings.
Basic Definitions
Computer Simulation refers to writing a program that captures the flow of events in the “real world” ranging from manufacturing to health care operations to restaurants. There are now several specialized software packages to support developing these models. For example, we might simulate the customer’s experience and actions from their arrival at the bank until their departure or their virtual arrival on a bank’s website.
A discrete event refers to only mimicking the flow where the actions in the flow are discrete events. The customer arrives at the restaurant, they are met by the host, seated, their order was taken, …., and check paid. The alternative is continuous – for example, emptying a bottle. This method involves rates and flow, and the best known is system dynamics by Jay Forester.
Monte Carlo refers to the use of random numbers to decide which option is selected at a decision or junction point that is inherently uncertain. For example, in an emergency department (ED) each new arrival might be one of three types of injury or illness that:
- Can be handled by regular ED staff and discharged.
- Will need to be admitted to the hospital.
- Requires emergency surgery
Associated with each discrete event is a probability of occurrence. For the 3 events for the ED, these might be 50%, 40%, and 10%.
Example of MCEDCS – Arrivals at the ED
To illustrate the core of MCEDCS we will use a simplified arrival and service at an ED.
Step 1: Generating an arrival.
Table 1 has arrivals for 5 people. The key concept is a random interarrival time for each person. We assume the first person arrives at time 0 (column 4), then we calculate the interarrival time between this arrival (at time 0) and the next arrival. To calculate this value, we use the “Monte Carlo method”. For this case, we assume the interarrival times follow a normal distribution with a mean of 3 and a standard deviation of 0.5 (rows 8 and 9). We first generate a random number between 0 and 1 using the Excel function “rand()”. We then convert this to an interarrival time following a normal distribution with a mean of 3 and a standard deviation of 0.5 with the Excel function “norm.inv”. The value 2.85 in the cell row 4 and column 3 is calculated with “norm.inv(0.3843,3,0.5)”. This is added to the arrival time of customer 1 to get an arrival time of 2.85.

Step 2: Classifying the Arrival.
Next, we randomly assign a type arrival for each arrival from the three types of ED arrivals provided above. Table 2 summarizes this information. For the three types of ED visits, we assign an integer in column 1. Column 3 is the probability of occurrence. Columns 4 and 5 have an upper bound and lower bound of values between 0 1 that belong to each type of ED visit. The first type (“regular”) has the values between 0 (lower bound) and 0.50 (upper bound) – this is called the range. The 0.50 is 0 + 0.50 (probability of occurrence. The lower bound for “admission” is 0.50 (the upper bound for “regular”) and the upper bound is 0.90 = (0.50 + 0.40). Observe the probabilities add to 1 and the first lower bound is 0 and the last upper bound is 1. We will use these ranges to randomly classify each arrival into one of three types of ED visits.

Table 3 illustrates how we randomly generate a type of arrival. Column 2 is a random number between 0 and 1 created with the Excel function “rand()”. If this value is between 0 and 0.50 (inclusive), then the type of ED visit is “regular” (1) with hours needed of 2. IF this value is greater than 0.50 and less than or equal to 0.90, then the type of ED visit is “admission” (2) with hours need of 3. IF this value is greater than 0.90 and less than or equal to 1.00, then the type of ED visit is “surgery” (3) with hours needed of 4. For the first arrival, the random number is 0.4991, this is between 0 and 0.5 (inclusive), hence the type of arrival is “regular”. For the fifth arrival, the random number is 0.8141 which is greater than 05. And less than or equal to 0.9, hence the type is “admission”. Table 4 has the Excel code to create Table 3.


Step 3: Finishing the sequence of events.
The simulation model would then continue to identify and log all major events for the patient until the patient exits ED; either released or turned over to another area of the hospital. For example, for “admission” a patient assigning to a holding area and the amount of time there; paperwork, then which hospital unit receives the patient. For surgery, is this an outpatient surgery that is scheduled for a later time, or hospital admission and surgery scheduled very soon (for example an appendectomy)? Assignment for scans (x-ray, cat scan, etc.)
Step 4: Analyzing the data.
The purpose of MCDECS is to create synthetic data to be analyzed. In this example, a key data point is the number of hours required each day and the number of arrivals for the day. For the day in Table 3, the number of ours is 13 (row 8, column 5 of Table 3) and the number of arrivals is 5. Figure 1 has a graph of 60 days of admissions with total hours required per day as the bar value and the color of the bar telling us if the number of arrivals is 4, 5, or 6.
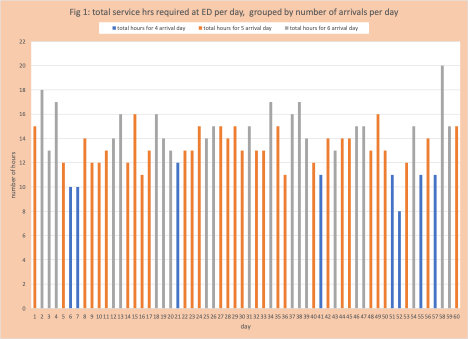
Conclusion
Monte Carlo Discrete Event Computer Simulation (MCDECS) developed by the OR/MS community with the advent of widely available general-purpose computers in the 1960s is a particularly powerful and flexible “tool of the trade” for a wide range of challenges in supply chain and operations management – from estimating capacity to setting COVID-19 protocols. This blog provided some basics on MCDECS, the next blog will use MCDECS to explain why limiting the size of a gathering helps reduce the spread of COVID-19.
Enjoyed this post? Subscribe or follow Arkieva on Linkedin, Twitter, and Facebook for blog updates.





