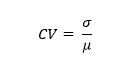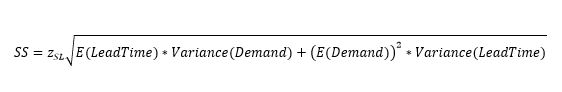In one of my previous posts, I wrote about using coefficient of variation (CV) as a predictor of forecastability. In this post, I will talk about how it can be used to indicate a sensitivity of lead time towards the safety stock calculations.
To quickly remind the reader first: The formula for CV = StdDev (σ) / Mean (µ)
And the formula for (cycle) safety stock is: (more detailed description here)
Where zSL represents a multiplier based on the specified service level. For a discussion on service levels, see my two part blog post (part 1 and part 2).
The Variance is square of the standard deviation (Variance = σ2).
E represents the expected value. In most cases, one assumes the expected value to be the average or the mean. However, if a business has an active forecasting process, the expected value of the demand can be the forecast and the Variance of demand can be calculated using the forecast error.
I can never remember this formula, so I always think of it like this:
Where the first term has to do with the variation in demand over the average lead time and the second term has to do with variation in supply with the average demand. Another way to think of it is that the first term deals with the demand variability (and by extension CV) and the second term deals with the supply variability.
Since I am focusing on the CV of demand, let me point out that the first term of the safety stock depends on the variability of demand (or forecast error where forecasting is used) and the second term depends on the mean demand. Generally speaking, when CV is high, forecast error is high as well.
Since safety stock depends on both supply and demand variability, one could impact it by working to reduce both. For example, to reduce demand variability, one might work on improving their forecast. But since demand is an external process and very difficult to control, I am going to treat it as a given and only discuss impacting supply side of the equation.
Now, if CV is high (or alternatively, the ratio of forecast error to mean demand is high which means the demand variance is high), then the first term in the safety stock calculation becomes more prominent. In this case, the average lead time is the main driver of the safety stock. The safety stock will go up or down considerably as the average lead time goes up or down.
If on the other hand the CV is low (or alternatively, the ratio of forecast error to mean demand is low which means the demand variance is low), then the second term becomes more prominent. This is even more so when the average demand is very significant. In this case, the safety stock calculation is more sensitive to the variability in the lead time or the supply. An increase or decrease in the variability of lead time would have more significant impact on the safety stock as compared to a similar change in average lead time.
What are the implications of this? If your product has a high CV or high forecast error, work on reducing the lead time. This could mean, positioning the safety stock closer to the customer, creating strategically placed inventory buffers to break the chain to reduce the lead time etc. If your product has a low CV or low forecast error, work on eliminating the variability in the supply of the product. This could mean working on processes, getting more reliable and higher quality suppliers etc.
This is not to say that you should only improve one of the three things. Assuming mean demand is a given, all three levers (demand variability via forecast accuracy, mean lead time, lead time variability) are fair game for improvements. It is easy to see that if one can make demand forecast more accurate while reducing lead times as well as lead time variability, they should do so.
Have you experimented with this within your supply chain? If so, I am interested in hearing from you.
Like this blog? Please share with colleagues and also follow us on LinkedIn or Twitter and we will send you notifications on all future blogs.