Summary: The spread of the COVID-19 virus is a major concern of everyone.  Typically, two critical questions are being asked: why it seemed to grow so quickly over the last few weeks and what is the impact of social distancing.  Of course, the dominant question is estimated as to the number of infected people and the impact on health care facilities.  This blog provides a kitchen table explanation of “rapid growth” and how social distancing might dampen growth.  No predictions are made with regards to the current COVID-19 outbreak, the formal mathematical expression is “exponential growth”.  There is no mathematics in this blog other than some calculations in Excel. Essentially the rate of growth is proportional to the number of people in the selected group (in this case active with COVID-19) and the key control valve is the spread factor.  In practice substantially more complex models are used, the purpose here is to explain the core concepts. As it turns out this type of growth (and the associated S curve) often applies in estimating demand when new technology is introduced.  An earlier blog provided an overview of the impact of the COVID-19 on supply chains and future blogs will do a deeper dive.

Additionally, Arkieva COO, Sujit Singh, participated in a town hall meeting titled: “Forecasting & Planning During the Chaos of a Global Pandemic”

Introduction:

Over the past week, we have seen a significant increase in the number of confirmed cases of COVID-19.  On 3/17/2020 at 1pm, the number of cases reported in the US was 5,000 up from under 100 at the start of March.  On 3/18/2020 at 8am the NY Times reported a total of 1500 people with COVID-19 in New York on 3/16/2020, up from 950 the day before. A recent study (model) out of London generated some eye-catching headlines.

I just returned from Phoenix Arizona where I was visiting my parents (88 and 91) and in chatting with them and their friends (similar in age), two questions that were asked were

  1. How could it grow so fast?
  2. Why social distancing?

Rapid Growth versus Steady Growth:

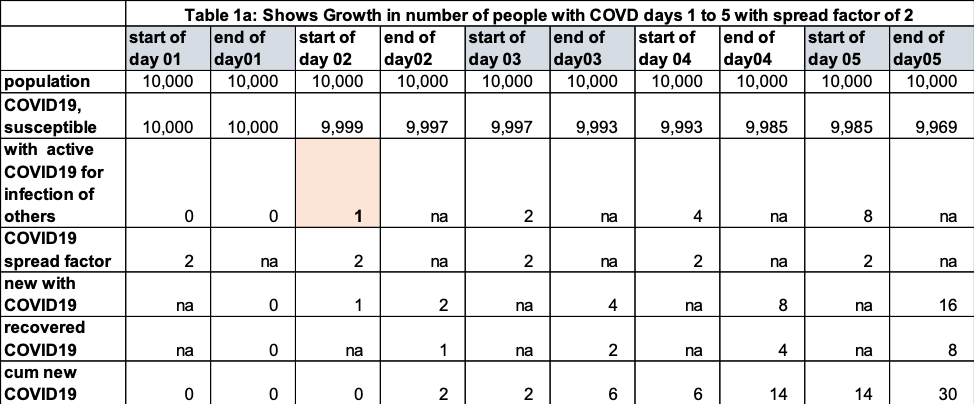
The mathematical term for the type of increases we have seen is the “exponential growth” curve where the rate of growth is proportional to the number in the set of interest.  I’ll use the following example which makes use of Table 1a and Table 1b. Table 1a has 10 columns: two columns each for the first 5 days of tracking COVID-19 spread, one column for the start of the day, and one column for the end of the day.  Table 2a covers days 6 to 10.  The rows are:

  1. Population: total population in ARK (stays at 10,000)
  2. Number in the population who have never had COVID-19 – called susceptible
  3. Number in population with active COVID-19 and able to infect others.
  4. COVID-19 spread factor (explained later)
  5. The number of people in ARK that have recovered from COVID-19 (can no longer spread COVID-19 and can no longer be infected).
  6. Cumulative cases of COVID-19 from Day 1 to current Day

rapid growth covid19

 

rapid growth covid19

Now let’s go day by day

  1. Day 1 Start: There are 10,000 people in ARK and zero people have COVID1-9.  Therefore the number of new COVID-19 cases at the end of day 1 must be ZERO since there is no opportunity for others to catch it.
  2. Day 1 end: Number of new active cases of COVID-19 is zero, the number of people never had COVID-19 10,000.
  3. Day 2 Start: Someone from ARK goes to the next town overnight to buy milk and returns with COVID-19. Now we have 1 active person that can spread COVID-19 and 9,999 who are susceptible to getting COVID-19.
  4. Day 2 End: The first item calculated is “spread” of COVID-19 – how many new cases occurred during day 2. The COVID-19 spread factor in this model is 2, which means that each person active with COVID-19 will spread it to two other people.  At the end of day 2, we have two new COVID-19 cases.  We are assuming any person that has COVID-19 at the start of the day is recovered by the end of the day.  The value in “recovered COVID-19” for Day 2 end is 1.  The cumulative new cases at the end of day 2 are 2 (we do not count the person who brought COVID-19 to ARK as new). 
  5. Start of Day3: 9,997 people are susceptible; 2 people are active and will spread COVID-19. The spread factor is 2, so 4 (2×2) new people will have COVID-19 at the end of day 3.
  6. End of Day3: recovered is 2, new is 4, cumulative is 6.
  7. Day 4: 9,993 susceptive, active with COVID-19 is 4, number of new cases is 8 (=2×4), recovered is 4 (number at the start of day 4), cumulative is 14 (=2+4+8)
  8. Day 5: 9,985 susceptible, active is 8, the number of new cases is 16 (=2×8), recovered is 8, cumulative is 30.

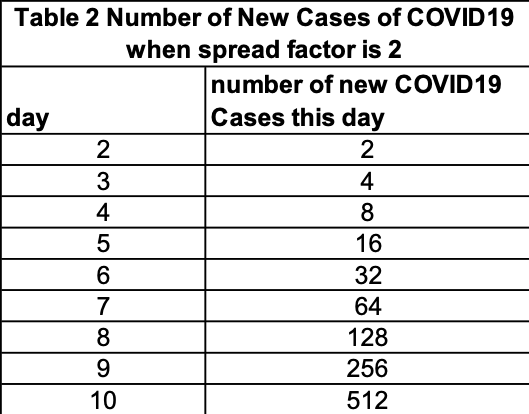
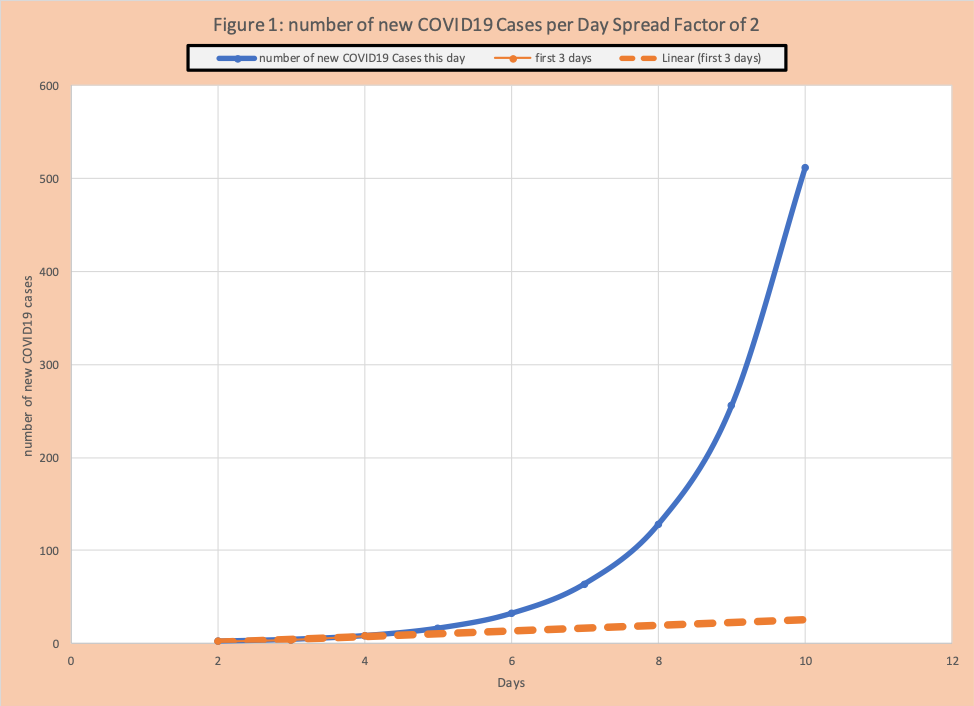
Observe in 4 days we have gone from 2 new cases (day 2) to 16 new cases (day 5).  Continuing the same logic on Day 10 (Table 1b) we have 256 new cases.  It would be helpful to have the formula to calculate the number of new cases on a given day without going day by day. This formula (in Excel notation) is power (2, (day-1)) = 2(day-1). Table 2 has this value for days 2 to 10.  Figure 1 has a graph of this information.  The first 3 days of observations are in orange and a best fit straight line is calculated for these first three.  Observe after three days, the straight line (“steady” growth) is a pretty good fit.  By day 8 its predictive power is poor since the growth is “rapid”).

rapid growth covid19

rapid growth covid19

Observe as the spread factor gets larger, the growth is faster and if the spread factor is smaller the growth is slower.

Social Distancing and Dampening Growth

The purpose of social distancing is to reduce the spread factor and dampen growth.  Figure 2 shows the growth of COVID-19 if the spread factor is reduced from 2 to 1.1 from day 1.

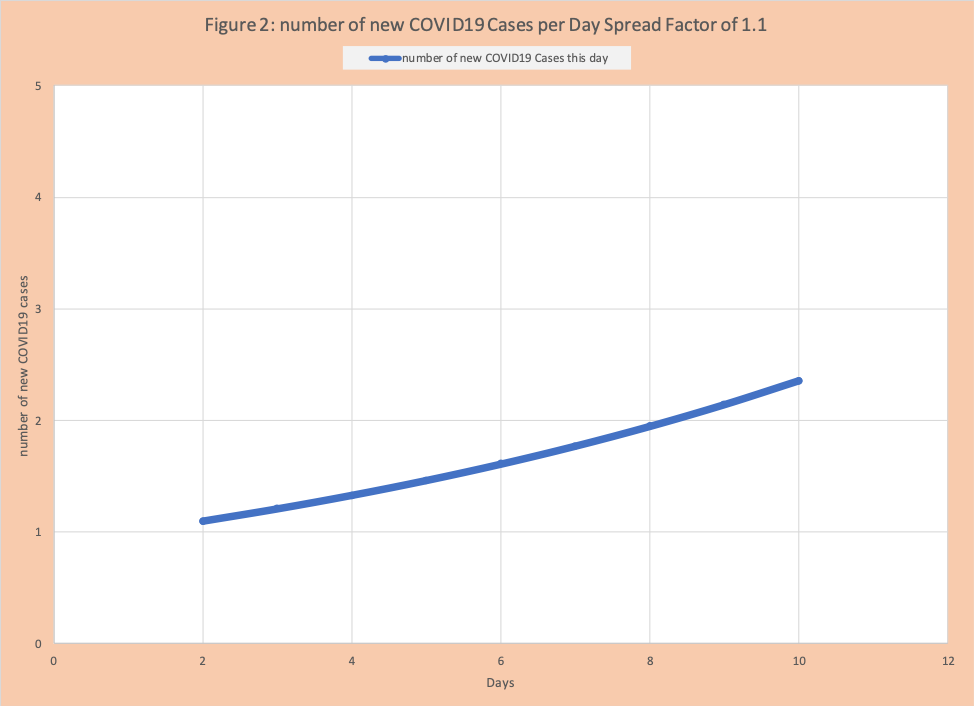
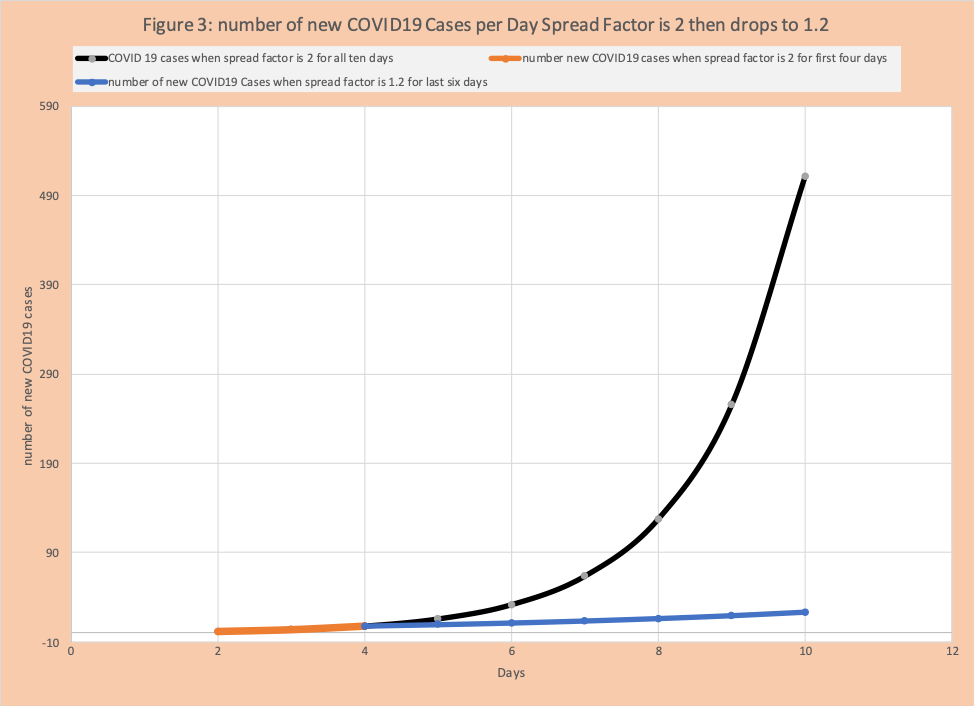
rapid growth covid19

However, typically actions to dampen occur well after day 1.  We want to understand this impact. Figure 3 shows the growth of COVID-19 when the spread factor is 2 for days 1 to 4 and then is reduced to 1.2 for days 5 to 10.   Figure 3 also has the original growth if the spread factor had remained 2 for the entire 2 days for contrast. We see the impact of changing the spread factor.

rapid growth covid19

Conclusion and Additional information

The purpose of this blog was to provide a few easy to follow examples on “raid growth” and dampening simply to take some of the mystery out of the current COVID-19 discussions.  The purpose was not to provide a rigorous discussion of infectious disease modeling.

For up to date information on the spread of COVID-19.

For a more formal discussion of this topic that is still easy to follow we refer the readers to Coronavirus and Flattening the Curve

Dangerous Numbers

Coronavirus by the Numbers

More detailed information can be found here.

Enjoyed this post? Subscribe or follow Arkieva on Linkedin, Twitter, and Facebook for blog updates.