National Puzzle Day – Solving Sudoku Puzzle Using Optimization in Arkieva

I learned this morning from my LinkedIn feed that January 29 is national puzzle day. So, we decided to put out a fun blog to mark the occasion. We have tried to solve Sudoku using a Mixed Integer Program (MIP). This blog is unrelated to Supply Chain although we use the technique used here to solve supply chain problems. Please enjoy!

From Wikipedia: Sudoku is a logic-based, combinatorial number-placement puzzle. The objective is to fill a 9×9 grid with digits so that each column, each row, and each of the nine 3×3 sub-grids that compose the grid (also called “boxes”, “blocks”, “regions”, or “sub-squares”) contains all of the digits from 1 to 9. The puzzle setter provides a partially completed grid, which typically has a unique solution. Completed puzzles are always a type of Latin square with an additional constraint on the contents of individual regions. For example, the same single integer may not appear twice in the same 9×9 playing board row or column or in any of the nine 3×3 subregions of the 9×9 playing board.

Problem Statement:

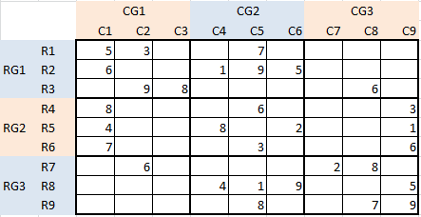
Populate the grid below such that:

Each Row contains all digits from 1 through 9 exactly once.
Each Column contains all digits from 1 through 9 exactly once.
Each 3×3 sub-grid (or box) as highlighted by bolder boundaries contains all digits from 1 through 9 exactly once. In the picture below, these are color-coded. Example: Rows R1-R3 belong to Row Group 1; Columns C4-C6 belong to Column Group 2 etc.

Model Definition: Domains

Rows (r): R1 through R9
Columns (c): C1 through C9
Box (b) : B1 through B9
Digits (d): D1 through D9

Model Definition: Variable(s)

Output_r,c,d is a binary (0,1) variable that represents the calculated output for a given row r, column c, and digit d. An absence of a combination indicates that the value for that cell was not provided. In cells where an input value was provided, the output must match the input.

An extra dimension box(b) is needed. This will allow us to add the constraint that every digit is allowed once and exactly once in a box.

Model Definition: Constraints

Constraint 1: Upper Bound of Output_r,c,d = Lower Bound of Output_r,c,d in cells where input is provided (this fixes the value of this variable is equal to the input).

Constraint 2: Every digit must appear once and exactly once in every column. How to say this in a language that the LP understands? Since we have defined our variables as binaries, here is a way to say it. For output variable, the sum of the binaries across a row for any given column and digit combination digit equals exactly 1 (If it equals less than 1 (=0), then that digit did not occur in the column anywhere, which is not allowed; If it equals more than 1, then that digit appeared more than once, which is not allowed either).

The equation below then is the same as saying that each digit occurs once and exactly once in a row.

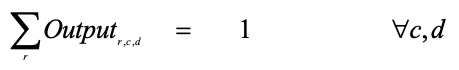
Constraint 3: Every digit must appear once and exactly once in every row. This implies that for the output variable, the sum of the binaries across a column for each row, for each digit equals exactly 1. This is the same as saying that each digit occurs once and exactly once in a column. By applying thinking that is like Constraint 2, we get the equation shown below.

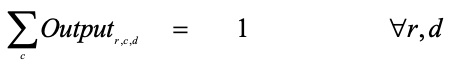
Constraint 4: Every digit must appear once and exactly once in every box. This implies that for the output variable, the sum of the binaries within each box, for each digit equals exactly 1. This is the same as saying that each digit occurs once and exactly once in each 3×3 box.

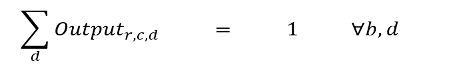
An additional requirement for this constraint is to make the model understand which row and column combinations are in which box.

Constraint 5: Only one digit can populate one cell. The set of equations above will allow a particular cell (say Row 5 – column 3) to have both 6 and 1 in it. This is the unwritten constraint in the problem. Human beings can intuitively grasp that only one number will go in each cell. Computers need everything to be stated explicitly. The equation below does the job.

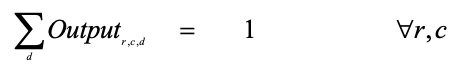
Since LP solves a simultaneous set of equations or constraints, the sequence of the constraints above does not matter. They can be entered in any sequence.

So, now that we have the model, we can put it to the test. We got an input problem from a website, feed it as an input, and see what the model does. Below is the first example.

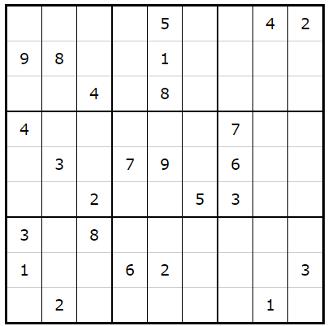
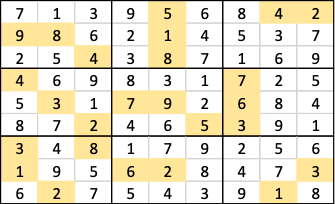
Here is the answer from the model in Arkieva. Yellow cells indicate the inputs.

Here is a ‘super hard’ problem as per the website.

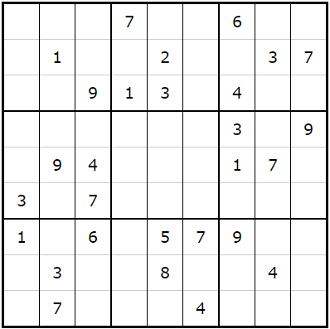
Here is the output from the Arkieva Model.

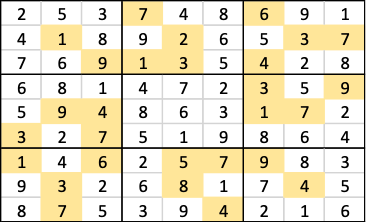
Here is a problem described as ‘impossible’ on the website.

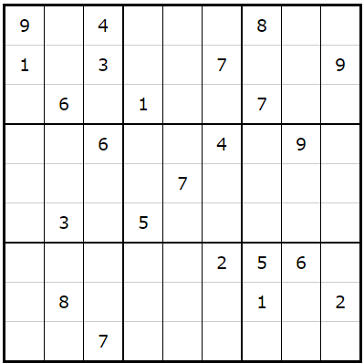
Here is the output from the Arkieva Model.

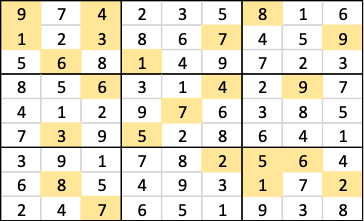
What if only 1 cell was populated in input?

Here is the output from the Arkieva Model.

And finally, what if all the cells were blank in the starting problem. Because of the equations above, the model would still find a random solution that satisfies all the constraints.