A colleague and I were talking recently, and the conversation turned to what is the relationship between Mean Absolute Deviation (MAD) and the Standard Deviation (STDEV). They specifically mentioned reading somewhere that STDEV (σ) ≈ 1.25*MAD.

In this post, I will explain to you the math behind that approximation, which by the way, only applies when the error terms (difference between observed and predicted) are normally distributed.

First, let us define these terms mathematically.

For a random variable with probability density function f(x),

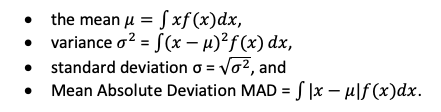
Mean Absolute Definition MAD graphic1

All the integrals have limits based on the range of the variable.  For a normal distribution, the limits are -∞ and +∞.

Read More: How to Report Forecast Accuracy to Management

The best estimates of these two quantities are:

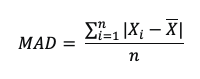
Mean Absolute Definition MAD graphic2

And

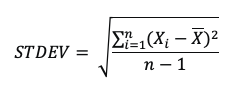
Mean Absolute Definition MAD graphic3

Where n is the number of observations, and Xi are the different observations from 1 to n.

Since we are assuming a normal distribution for this example, it is helpful to remember that the density function of a normally distributed random variable ‘x’ is:

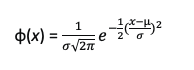
Mean Absolute Definition MAD graphic4

where σ is the standard deviation of the variable x.

Read More: Seasonal Model Forecasting with Seasonal Methods

With those definitions in place, let us look at the following.

If X is a normally distributed random variable with mean μ, let Y = X – μ.

Then, it follows that Y is a normally distributed random variable with mean 0, and the expected value of |Y| is the mean absolute deviation of X (=|X-µ|).  The density function of Y can be written as:

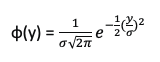
Mean Absolute Definition MAD graphic5

where σ is the standard deviation and the mean is 0.  The expected value of |Y| is given by:

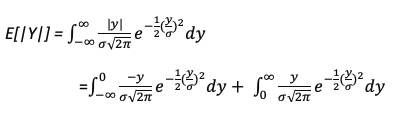
Mean Absolute Definition MAD graphic6

These two integrals have the same value as one goes from -infinity (-∞) to 0, and the other goes from 0 to infinity (∞). So, we can just evaluate:

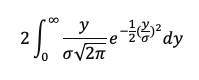
Mean Absolute Definition MAD graphic7

 

For calculating the limits, remember that e-∞ = 0 and e0 = 1. The above then equals:

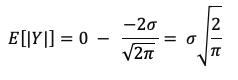
Mean Absolute Definition MAD graphic9

Since σ represents STDEV it follows that MAD is standard deviation times Mean Absolute Definition MAD graphic10  , which is roughly equal to 0.798. By simple math, it then follows that:

STDEV ≈ (1/0.798) * MAD

                                     ≈ 1.25 * MAD

 
Enjoyed this post? Subscribe or follow Arkieva on Linkedin, Twitter, and Facebook for blog updates.