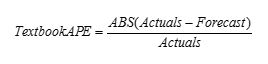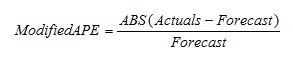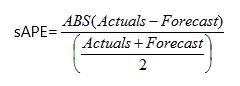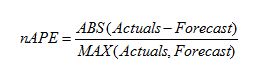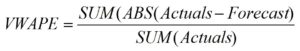I saw this news article on CNN (here) about our planet’s earth bigger, older cousin. Quite an interesting discovery if you ask me. However, it got me thinking about the family tree of Mean Absolute Forecast Error (MAPE), a subject that I am a little bit familiar with.

A few weeks ago, I wrote about the two sides of the MAPE coin. After the post, I got a lot of feedback around the varying ways practitioners and researchers have modified the MAPE. For me, these variations represent the family tree of MAPE 🙂

As mentioned in the previous article, the MAPE consists of two parts: M and APE. The formula for APE is:

Formula for calculating APE a part of MAPE

The M stands for mean (or average) and is simply the average of the calculated APE numbers across different periods, and is derived by dividing the APE by the number of periods considered. In all the formulas shown below, I am leaving out the M part of the formula on purpose.

MAPE has many criticisms around its asymmetry as well as how it performs near extremes (for example when actuals = 0). Most of the debate is around whether or not the denominator (Actuals) is the right one. This debate has over time resulted in the variations described below.

Divide by Forecast: This definition changes the denominator from Actuals to forecast. People who favor this method are concerned with the fact that MAPE encourages under-forecasting. However, they do not realize they fix one problem and create another. Dividing the error by forecast simply favors larger forecasts as they result in lower percentage error. The formula is:

Variation of MAPE is ModifiedAPE

I have seen this method used in many CPG companies.

Dividing by the mean of Actual and Forecast: This definition changes the denominator to

[(Actuals + Forecast) / 2]. Proponents of this formula typically lament the inherent asymmetry or bias in the MAPE formula (it favors low forecast) and tries to counter by changing the denominator in the manner described above. The claim is this makes the measure more symmetric or unbiased and therefore goes by the name of symmetric MAPE (or sMAPE) or Unbiased MAPE (or UMAPE or even UAPE). The formula is:

variation of MAPE is sAPE

For what it is worth, this formula, while more symmetric than the original MAPE, is still not completely unbiased. I have not seen it used many places.

Dividing by the maximum of Actual and Forecast: This definition changes the denominator to [MAX (Actuals, Forecast)]. Folks who prefer this formula tout the fact it is stricter in how it reports the error and does not allow anyone with consistent under or over forecasting. It does not necessarily concern itself with symmetry at all. It is recognized as the Normalized MAPE or nMAPE. The formula is:

Variation of MAPE is nAPE

Take the median instead of the mean: This definition keeps the original formula for the APE portion of the calculation; but in the end, it looks for the median value (or the middle value) versus the mean value of the overall distribution. This typically works better when the underlying data is skewed and the corresponding APE values are not normally distributed. In this case, one should take the median value into consideration. As you can imagine, this method is called Median APE or MdAPE.

I must give credit to Hans Levenbach who posted this formula in a recent LinkedIn discussion. I have never used this metric myself.

Weighted MAPE: This is one of my favorite ways of measuring and reporting forecast accuracy, and I discussed it in some detail (here). There are many variations, but the most popular one is the volume weighted MAPE and the formula is very concise:

variation of MAPE is VWAPE

This metric is very popular and also highly recommended for use when reporting forecast accuracy to top management.

I am sure I have missed a few variations of MAPE and also very sure that new ones will be invented in the future. If anything, this points to the popularity of MAPE as a forecast accuracy measurement.

Do you use a different version of MAPE? If so, I am interested in hearing from you.

Like this blog? Follow us on LinkedIn or Twitter and we will send you notifications on all future blogs.

PS: I originally wanted to name this blog “MAPE and his/her/its cousins”. But could not decide which gender to use. What do you think? Please provide your comment if you do not mind indulging me a bit.