
The Supply chain is driven by demand, supply, and inventory planning. Under demand planning, the importance of sales forecasting is undeniable. It provides a basis for the production process regulating quantities, inventory and maximizes the efficiency of the resources available.
The sales forecasting process is often focused on estimating sale quantities for production planning.
But what if we were more interested in the chances of sales happening rather than estimating quantities of future sales?
This type of sales prediction could be beneficial for sales teams interested in cold calling and customer interaction. While there are many tried and tested methods used for forecasting, a fairly unused method is the Markov Chain method.
Read: Demand Forecasting: The Art and Science That Keeps You Guessing
What is a Markov Chain?
Markov Chain is a hermit in the world of statistics, but its potential is immense. A Markov Chain is a stochastic model describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event.
Lost in translation?
Well let’s put it this way, Markov Chains are mathematical systems that hop or “transition” from one “state” (a situation or set of values) to another. Hence if we have the total number of states of a system (called state space), it is possible to mimic the systems phenomena and provide long term statistics.
Still lost? Let’s try an example:
Markov Chain Example
The Land of Oz is blessed by many things, but not by good weather. They never have two nice days in a row. If they have a nice day, they are just as likely to have snow as rain the next day. If they have snow or rain, they have an even chance of having the same the next day. If there is a change from snow or rain, only half of the time does this change to a nice day. With this information, we form a Markov chain as follows: we take states as the kinds of weather Rain(R), Nice (N), and Snow (S). From the above information, we determine the transition probabilities. These are most conveniently represented in a square array as:
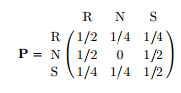
The matrix P is called the transition probability matrix which basically shows the probabilities of transitioning from one state to another. Markov Chains are such that given the present state, the future is conditionally independent of the past states.
So if we assume the initial state of the system to be, then the state vector for the next time period would be:
xn+1 = xn .P
Read Also: The ‘Secret Sauce’ to Improving Demand Planning
How do we use the Markov Chain for Sales Prediction?
Let’s consider an organization which sells raw materials as products to its customers. Now let’s take the sales history of one product to a particular customer:
| Product Name | Shipment Quantity | Date of Shipment |
| Product 1 | 500 | 1/2/17 |
| Product 1 | 24 | 1/4/17 |
| Product 1 | 139 | 1/7/17 |
So, to establish a Markov chain, we need to base it on a set time series or time buckets. Since we’re experimenting with data at a high detail level, we’ll consider daily time buckets.
Since we’re not going to consider the quantity being shipped, there are only 2 possible states in this system:
1 – Sale was made on that day
0 – Sale was not made on that day
Let’s format the sales history to reflect the states over a week in January:
| Date | State |
| 1/1/17 | 0 |
| 1/2/17 | 1 |
| 1/3/17 | 0 |
| 1/4/17 | 1 |
| 1/5/17 | 0 |
| 1/6/17 | 0 |
| 1/7/17 | 1 |
The Transition Probability matrix would look as so:
P =
| No Sale | Sale | |
| No Sale | 0.25 | 0.75 |
| Sale | 1 | 0 |
Now if we consider the initial state to be the state on 1/17/17 which is:
X =
| No Sale | Sale |
| 0 | 1 |
Therefore according to the Markov property, the state of the system on 1/8/17 is:
xn+1 = xn .P
=
| No Sale | Sale |
| 1 | 0 |
Related: 5 Reasons Collaboration Can Make Your Forecast Better
This means the Markov chain predicts a no sale on 1/8/17
Using the Markov chain, the sales department can develop an elaborate system gives them an advantage in predicting when a customer should have placed an order. Imagine a hectic day at the office for the operations team at the customer side, where customers haven’t placed orders for extra raw materials. An unexpected call from the sales team to find out why the customer hasn’t placed an order would bolster a strong client-customer relationship. Customer approval and trust is the foundation of any successful business and Markov Chains could help.
Sounds simple enough, but before you go throwing away your normal forecasting or prediction methods out the window, this example uses a basic supply chain system. A normal supply chain system would be influenced by quantities, locations, trends, overrides and large amounts of data. So this is a concept definitely worth exploring and rest assured, Arkieva is working on it. Watch this space for more about the elusive Markov Chain!





